Под воздействием статьей с хабрахабр, а так же отличной книги "Электроника - теория и практика", я решил так же сделать разбор цепи и сохранить у себя.
Эти все результаты можно получить с помощью любой программы моделирования электрических схем, статья просто образовательного характера, а так же показывает некоторые алгоритмы используемые в программах моделирования. В статье я покажу результаты моделирования в LTSpice.
И так, исходная схема:
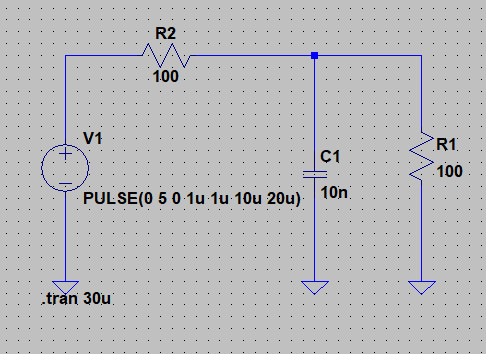
Схема состоит из источника напряжения(Us, V1, 5В), резисторов R1 и R2 по 100Ом и конденсатора 10нФ. Если не рассматривать переходные процессы, то резисторы представляют собой делитель напряжения, конденсатор - разрыв для постоянного тока, а в случае отключения V1(Us) источника, то сам становится источником, заряженным до напряжения 2.5В и разряжающегося через сопротивления R1 и R2. Но, что, если V1(Us) не постоянный источник напряжения, а например источник с нестандартной формой сигнала, не синусоида. Понятно, что сигнал любой формы можно разложить в ряд Фурье (пример ниже):
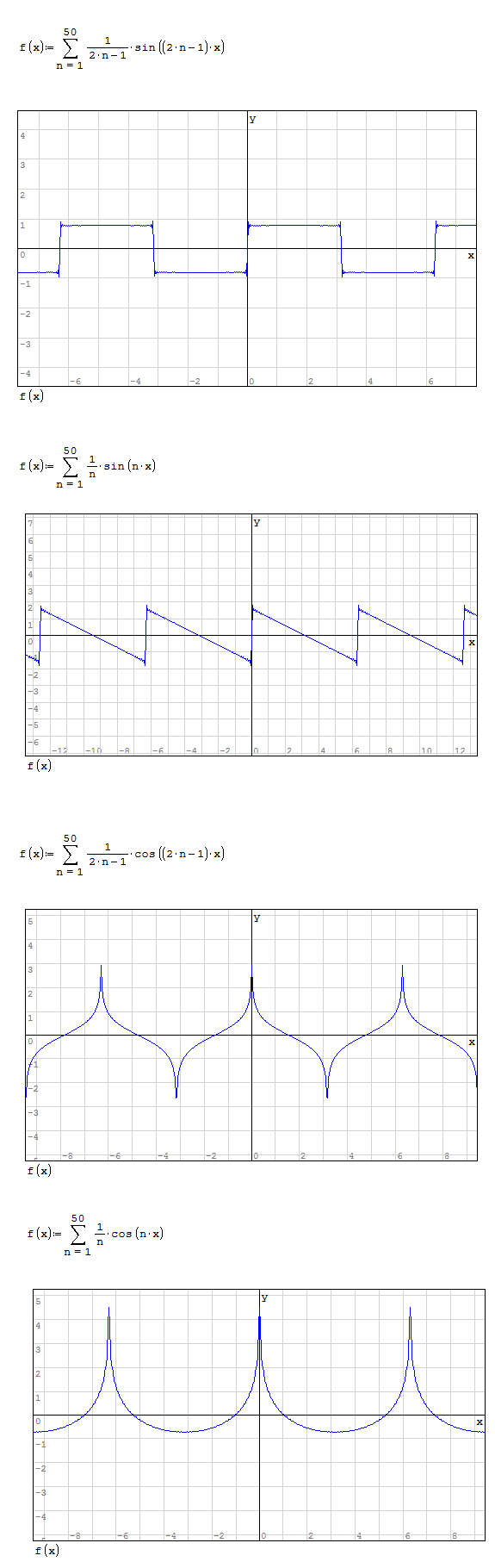
и применить формулы для синусоидальных колебаний и мнимые числа. Но пойдем другим путем.
Источник в схеме - это: нарастание напряжения от 0 до 5В за 1мкс, 9мкс источник поддерживает 5В и за 1мкс падение уровня напряжения до 0В и 9мкс напряжения нет.
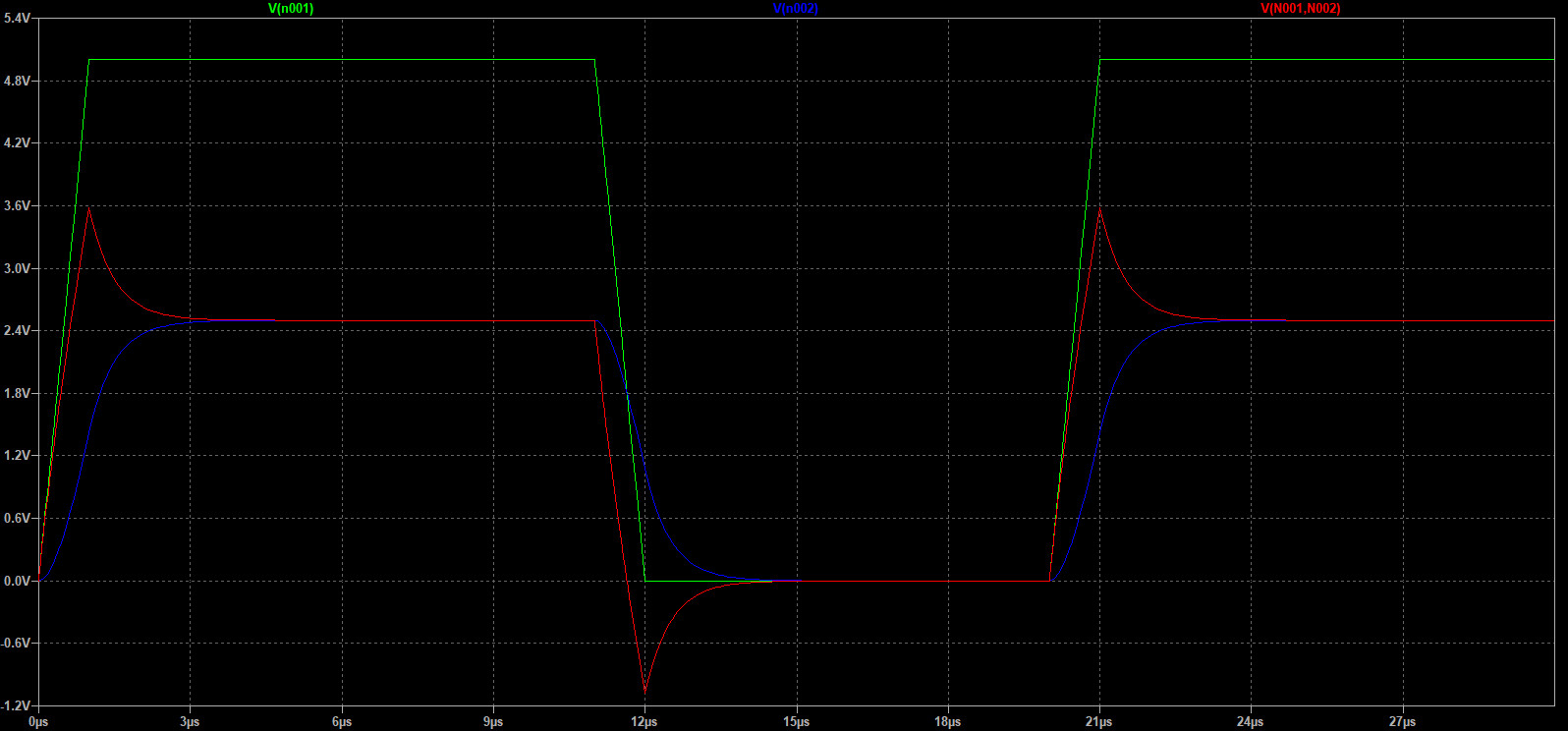
Смоделируем результат работы схемы в LTSpice:
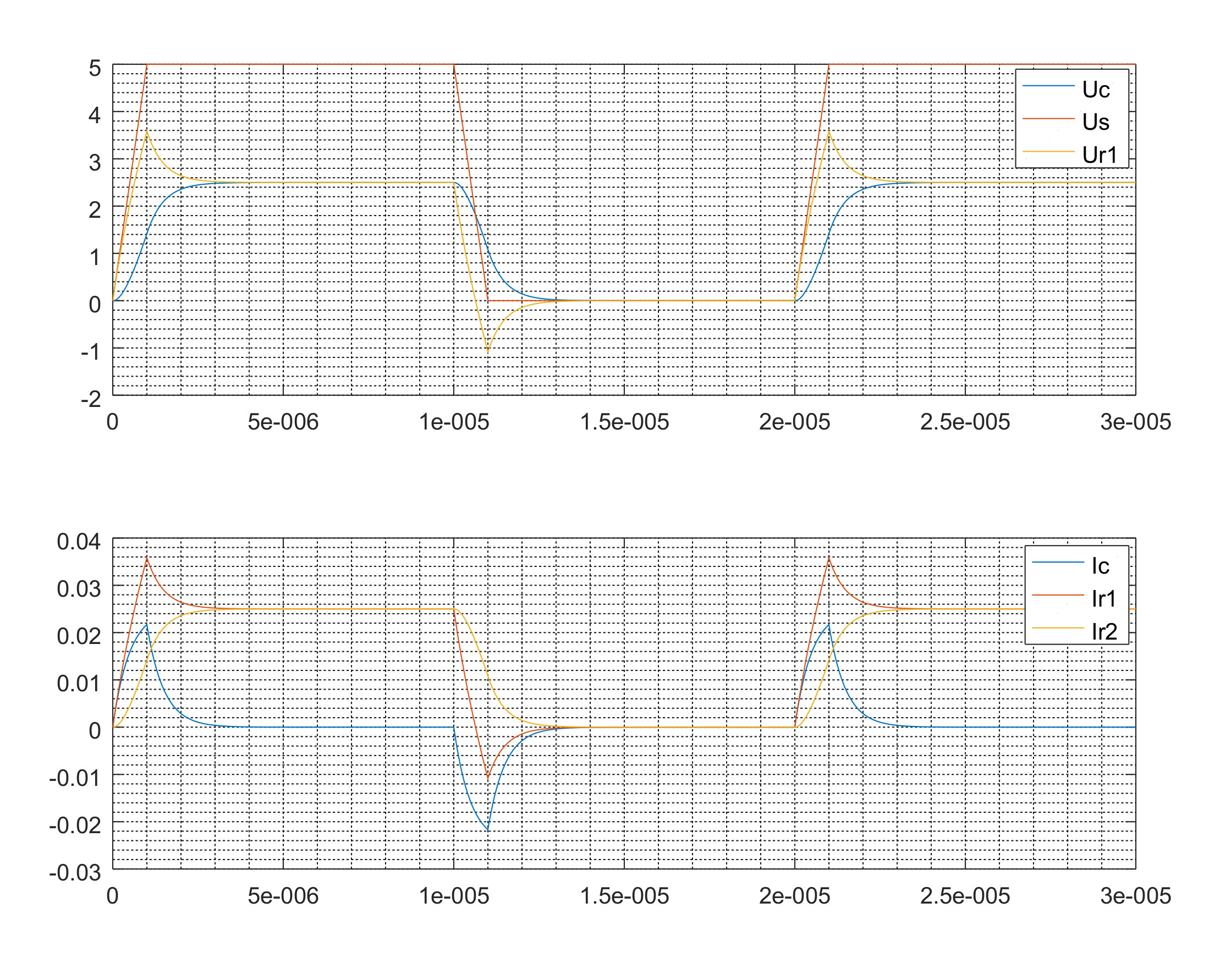
- Результат моделирования для V1, Ur2, Uc - напряжение источника(зеленый график), падение напряжения на R2(красный) и напряжение на обкладках конденсатора(синий график).
- Результат моделирования, но теперь по току V1, Ir2, Ic - напряжение источника(зеленый график), ток на R2(синий) и ток на конденсаторе(красный).
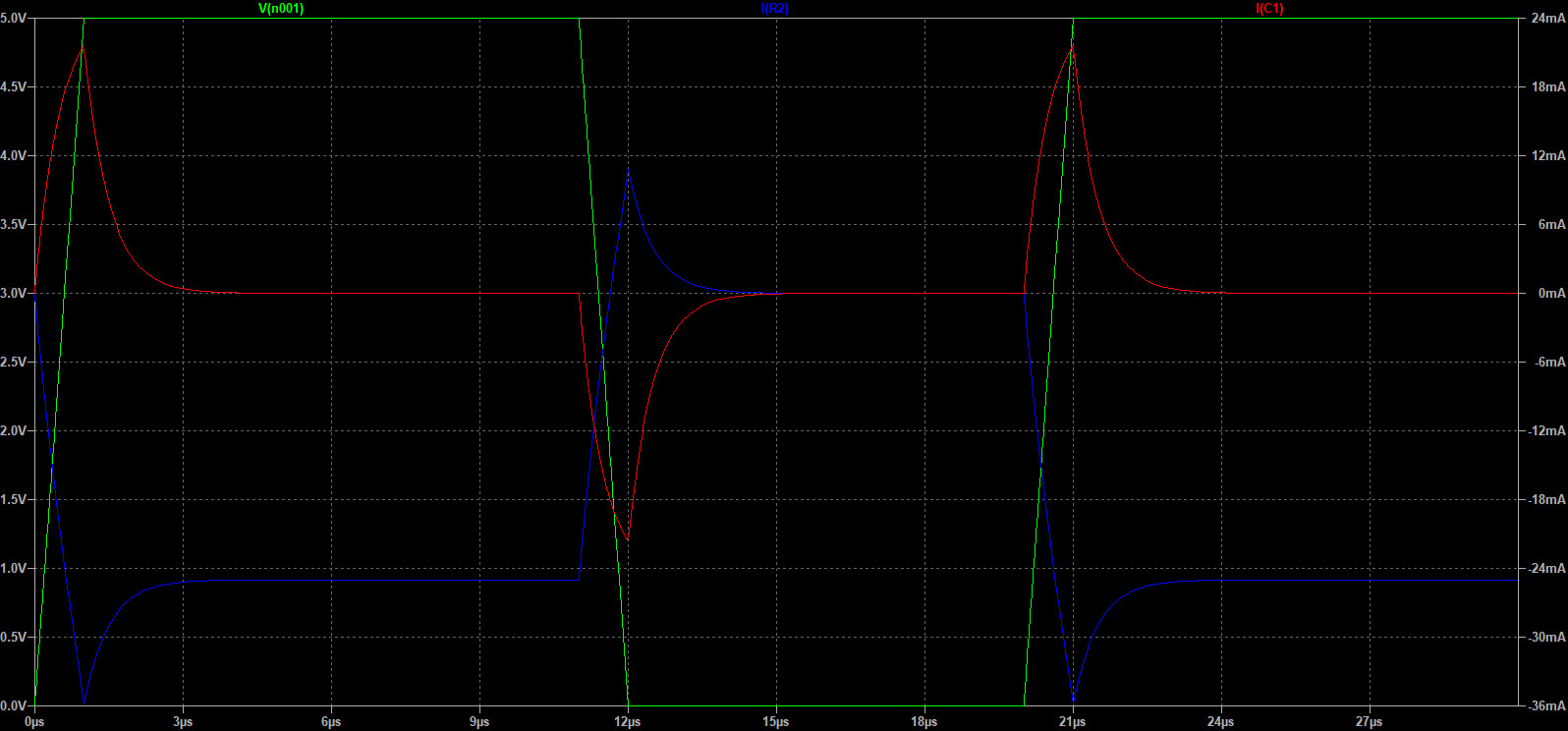
Как видно из графиков, в переходные моменты, при нарастании напряжения от источника, конденсатор представляет собой меньшее сопротивление чем R1, поэтому на R2 ток выше предполагаемого 5В/200Ом=0.025А, но в конечном итоге при завершении переходных процессов он именно таким и устанавливается. И наоборот при понижении уровня напряжения появляется обратный ток, связанный с разрядкой конденсатора.
А теперь рассчитаем схему и смоделируем ее в Octave.
Немного преобразую схему:
Составлю узловые и контурные уравнения. В схеме два контура - левый и правый. И два узла идентичных, т.е можно считать один узел.
В схеме есть: U1 - падение напряжения на R1, Uc - падение напряжения на емкости, U2 - падение напряжения на R2 и Us - источник напряжения. I1 - ток на R1, Ic - ток конденсатора, I2 - ток на R2.
Итого:
- \(U_1=R_1*I_1 (1)\)
- \(U_2=R_2*I_2 (2)\)
- \(U_c=\frac{1}{C}*\int I_c \, dt\)
- \(I_c=C*\frac{dU}{dt} (6)\)
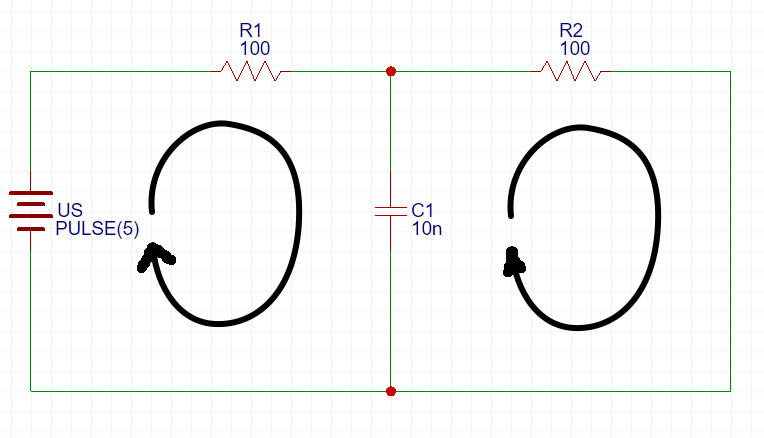
Левый контур:
\(U_s-U_1-U_c=0 (3)\)
Правый контур:
\(U_c-U_2=0 (5)\)
Узел:
\(I_1-I_c-I_2=0 (4)\)
откуда получаем:
- из (1): \(I_1=\frac{U_1}{R_1}\)
- из (2): \(I_2=\frac{U_2}{R_2}\)
- из (3): \(U_1=U_s-U_c\)
- из (5): \(U_2=U_c\)
- из (4): \(I_c=I_1-I_2=\frac{U_1}{R_1}-\frac{U_2}{R_2}=\frac{U_s-U_c}{R_1}-\frac{U_c}{R_2}\)
из (4) заменив Ic на (6) получаем:
- \(C*\frac{dU}{dt}=\frac{U_s-U_c}{R_1}-\frac{U_c}{R_2}\)
- \(\frac{dU}{dt}=\frac{U_s-U_c}{R_1*С}-\frac{U_c}{R_2*С}\)
все, теперь все есть, можно вычислить dU/dt методом Эйлера для решения дифференциальных уравнений:
\(X_i=X_{i-1}+h*\frac{dX_{i-1}}{dt}\)
Вот как будет выглядеть m файл для Octav для моделирования цепи:
1;
function result = Volt1(t)
VOLTAGE=5.0;
PERIOD=1*10^-6+9*10^-6+1*10^-6+9*10^-6;
PPERIOD=t-floor(t/PERIOD)*PERIOD;
RES = 0.0;
if (PPERIOD<(1*10^-6))
RES=VOLTAGE/(1*10^-6)*PPERIOD;
elseif (PPERIOD>=(1*10^-6) && PPERIOD<=(10*10^-6))
RES=VOLTAGE;
elseif (PPERIOD>(10*10^-6) && PPERIOD<(11*10^-6))
RES=VOLTAGE-VOLTAGE/(1*10^-6)*(PPERIOD-10*10^-6);
else
RES=0.0;
end
result = RES;
endfunction
function result = dUc_dt(c, r1, r2, Ui, Uc, iter)
result = (Ui(iter)-Uc(iter))/(r1*c)-(Uc(iter)/(r2*c));
endfunction
r1 = 100;
r2 = 100;
c = 10*10^-9;
delta=0.00000003;
steps=0.00006/delta;
E_y=[Volt1(0)];
E_c=[0.0];
I_c=[0.0];
I_r1=[0.0];
I_r2=[0.0];
U_r1=[0.0];
for entry = [2:1:steps],
E_y=[E_y; Volt1(entry*delta)];
E_c=[E_c, E_c(entry-1)+delta*dUc_dt(c, r1, r2, E_y, E_c, entry-1)];
I_c=[I_c, c*dUc_dt(c, r1, r2, E_y, E_c, entry)];
I_r1=[I_r1, (E_y(entry)-E_c(entry))/r1];
I_r2=[I_r2, (E_c(entry))/r2];
U_r1=[U_r1, I_r1(entry)*r1];
endfor
times=[];
for entry = [1:1:steps],
times=[times; entry*delta];
endfor
subplot (2, 1, 1);
plot(times, E_c, "-;Uc;", times, E_y, "-;Us;", times, U_r1, "-;Ur1;");
grid minor;
subplot (2, 1, 2);
plot(times, I_c, "-;Ic;", times, I_r1, "-;Ir1;", times, I_r2, "-;Ir2;");
grid minor;Volt1- функция для описания поведения источника напряжения в зависимости от времени.dUc_dt- функция вычисления части \(\frac{dX_{i-1}}{dt}\) в уравнении Эйлера.- эта строка
E_c(entry-1)+delta*dUc_dt(c, r1, r2, E_y, E_c, entry-1)непосредствеено само уравнение. Вычилсив его, мы можем вычислить и остальные величины.I_c=[I_c, c*dUc_dt(c, r1, r2, E_y, E_c, entry)]; I_r1=[I_r1, (E_y(entry)-E_c(entry))/r1]; I_r2=[I_r2, (E_c(entry))/r2]; U_r1=[U_r1, I_r1(entry)*r1];Все данные собираются в векторах и отрисовываются на графиках. Вот что получилось в результате(верхний график напряжений, нижний - токов):
Изменив функцию Volt1 на такой алгоритм:
function result = Volt1(t)
VOLTAGE=5.0;
PERIOD=20*10^-6;
PPERIOD=t-floor(t/PERIOD)*PERIOD;
RES = 0.0;
if (PPERIOD<=(5*10^-6))
RES=VOLTAGE/(5*10^-6)*PPERIOD;
elseif (PPERIOD>(5*10^-6) && PPERIOD<=(10*10^-6))
RES=VOLTAGE/(5*10^-6)*(PPERIOD-5*10^-6);
elseif (PPERIOD>(10*10^-6) && PPERIOD<=(15*10^-6))
RES=VOLTAGE/(5*10^-6)*(PPERIOD-10*10^-6);
else
RES=VOLTAGE/(5*10^-6)*(PPERIOD-15*10^-6);
end
result = RES;
endfunctionможем промоделировать поведение при пилообразном напряжении:
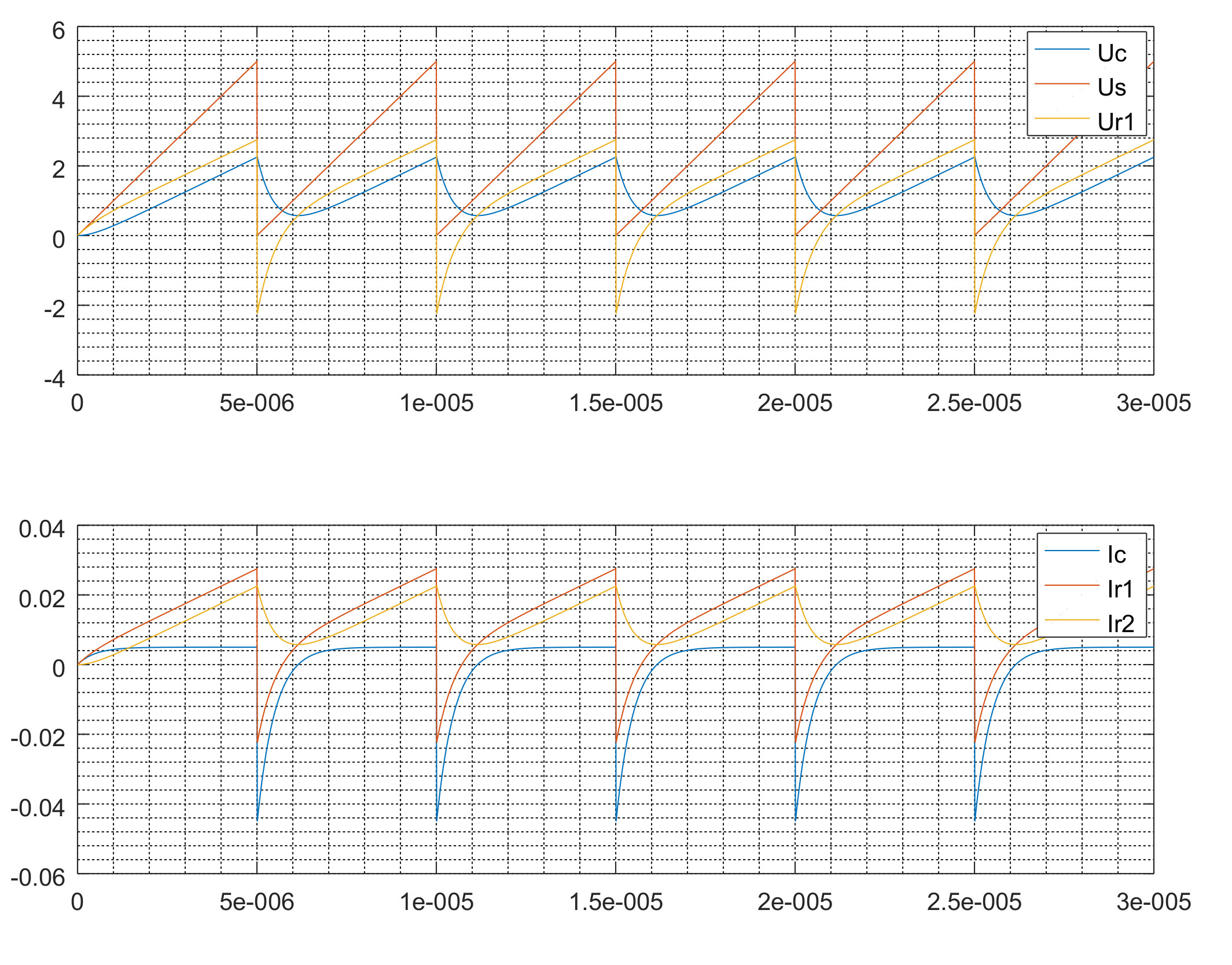
Графики от LtSpice похожи на графики от Octave.
