Моделирование электрической цепи в Octave. Часть 2

Электричество Схема Моделирование Octave

Продолжение темы моделирования электрической схемы в Octave. В прошлый раз рассматривалась схема с двумя контурами, содержащая конденсатор.

Попробую промоделировать другую схему, содержащую больше контуров.

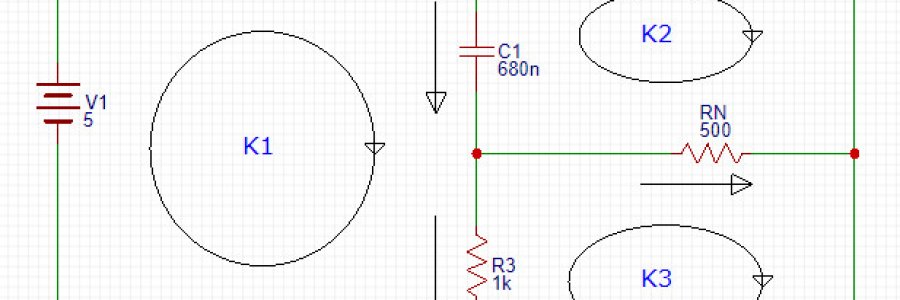
Схема для моделирования была взята из статьи про операционные усилители. Ниже приведена перерисованная по контурам схема:

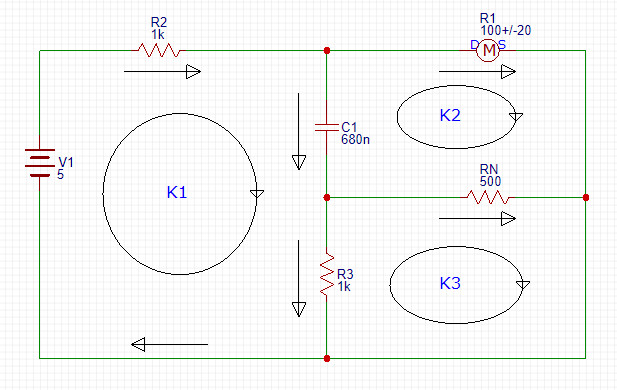
Схема для Octave

R1 - это микрофон, в моделировании он заменен переменным резистором, сопротивление которого колеблется в пределах 10-20Ом. Rn - это нагрузка, чем больше тем лучше. Для моделирования был выбран средний вариант.

Вот оригинал схемы:

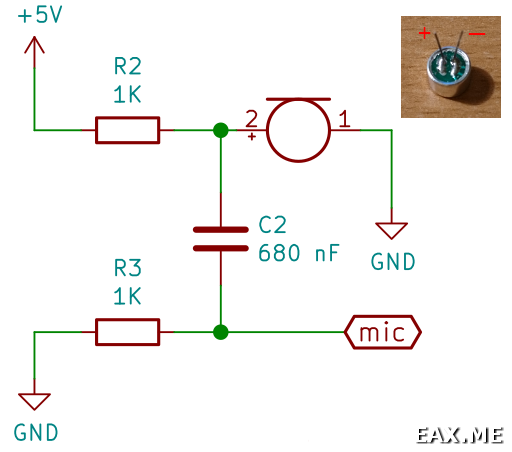
Как и в прошлый раз - моделирование в LTSpice:

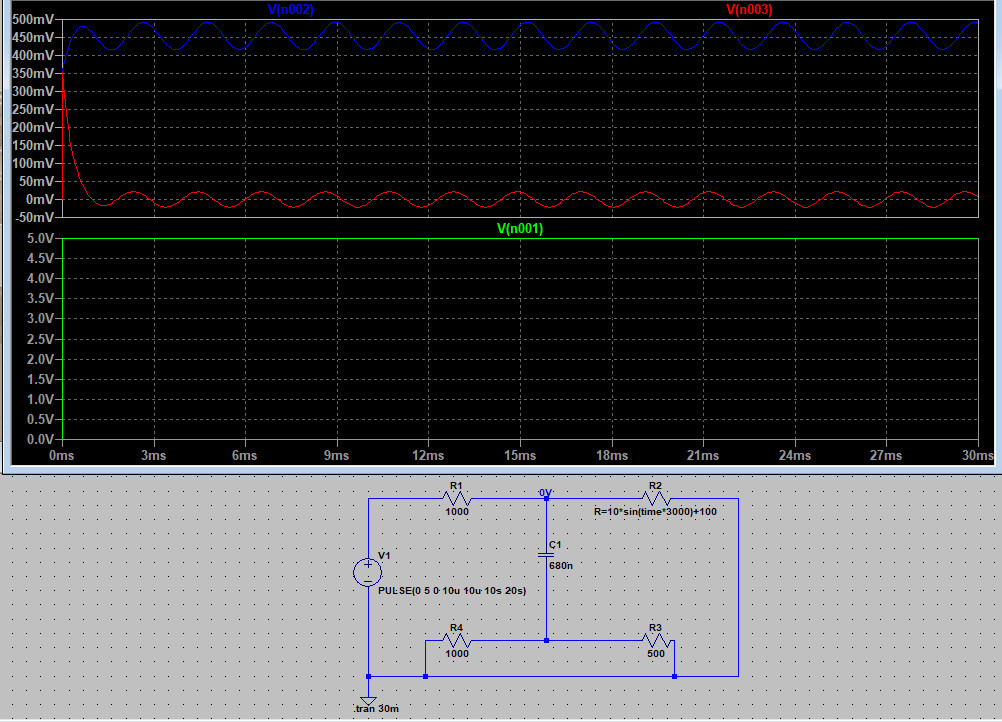
Моделирование

В LTspice в качестве электретного микрофона используется резистор, который изменяет сопротивление по формуле R=10*sin(time*3000)+100. На выходе схемы перед на Rn, можно увидеть отфильтрованный от постоянного напряжения сигнал, достаточно слабых колебаний, которые потом проходят через операционный усилитель. Но операционный усилитель вне текущей статьи, поэтому ограничусь Rn=500 Ом.

Тепер рассчет для моделирования. Формул много:

  • V1 - напряжение источника. Он включается не мгновенно, уровень напряжения нарастает до 5В в течении 1 микросекунды, линейно.

  • I1,I2,I3,In,Ic - токи через R1,R2,R3,Rn и конденсатор.

  • Uc - потенциал конденсатора относительно земли.

  • по первому контуру: (1) \(V_1-I_2*R_2-U_c-I_3*R_3=0\)

  • по второму контуру: (2) \(U_c-I_1*R_1+I_n*R_n=0\)

  • по третьему контуру: (3) \(I_3*R_3-I_n*R_n=0\)

  • по верхнему узлу: (4) \(I_2-I_c-I_1=0\)

  • по среднему узлу: (5) \(I_c-I_3-I_n=0\)

  • по нижнему узлу: (6) \(I_1+I_3+I_n-I_2=0\)

теперь приведение к виду Ic=f(Uc).

Из уравнения 3 получаю: \(I_n=I_3\frac{R_3}{R_n}\) (7) далее вывожу I3 через Ic из (5) путем подстановки In из (7): \(I_c-I_3-I_3\frac{R_3}{R_n}=0\) итого: \(I_3=\frac{I_c}{1+\frac{R_3}{R_n}}\) (8)

из уравнения (7) путем подстановки I3 из (8) нахожу зависимость In от Ic: \(I_n=\frac{I_c*R_n}{R_n+R_3}\) (9)

Имею I3, In выраженные через Ic, подставлю в (2) уравнение из (9): \(U_c-I_1*R_1+\frac{I_c*R_3*R_n}{R_n+R_3}=0\) откуда нахожу I1 зависимое от Ic и Uc: \(I_1=\frac{I_c*R_3*R_4}{R_1*R_n+R_1*R_3}+\frac{U_c}{R_1}\) (10).

Найду I2 из уравнения (4) подставив вместо I1 формулу (10): \(I_2=I_c+I_1=I_c+\frac{I_c*R_3*R_4}{R_1*R_n+R_1*R_3}+\frac{U_c}{R_1}\)

Теперь все токи: I1, I2, I3, In выражены через Ic, Uc, подставлю их в (1):

\(V_1-I_c*R_2-\frac{I_c*R_3*R_n*R_2}{R_1*R_n+R_1*R_3}-\frac{U_c*R_2}{R_1}-U_c-\frac{I_c*R_3*R_n}{R_n+R_3}=0\)

из формулы вывожу:

\(I_c=\frac{V_1-\frac{U_c*R_2}{R_1}-U_c}{R_2+\frac{R_3*R_n*R_2}{R_1*R_n+R_1*R_3}+\frac{R_3*R_n}{R_n+R_3}}\) (11)

ранее в предыдущей статье была озвучена формула: \(I_c=C*\frac{dU}{dt}\) которая показывает, что dU по dt можно вычислить, если формулу (11) разделить на C, т.е на емкость.

Вот как выглядит программа для Octave:

1;

function result = Volt1(t)
  VOLTAGE=5.0;
  RES = 0.0;
  if (t<(1*10^-6))
    RES=VOLTAGE/(1*10^-6)*t;
  else
    RES=VOLTAGE;
  end

  result = RES;
endfunction

function result = dUc_dt(c, r1, r2, r3, rn, Ui, Uc, iter)
  result = 1/c*(Ui(iter)-Uc(iter)*r2/r1(iter)-Uc(iter))/(r2+r3*rn*r2/(r1(iter)*rn+r1(iter)*r3)+r3*rn/(rn+r3));
endfunction

function res = R1_res(t)
    res = 20*sin(t*6000)+100;
endfunction

r2 = 1000;
c = 680*10^-9;
rn = 500;
r3 = 1000;
delta=0.000045;

steps=0.03/delta;
E_y=[Volt1(0)];
r1_y=[R1_res(0)];
E_c=[0.0];
I_c=[0.0];
I_n=[0.0];
U_n=[0.0];
for entry = [2:1:steps],
  E_y=[E_y; Volt1(entry*delta)];
  r1_y=[r1_y; R1_res(entry*delta)];
  E_c=[E_c, E_c(entry-1)+delta*dUc_dt(c, r1_y, r2, r3, rn, E_y, E_c, entry-1)];
  I_c=[I_c, c*dUc_dt(c, r1_y, r2, r3, rn, E_y, E_c, entry-1)];
  I_n=[I_n, I_c(entry)*r3/(rn+r3)];
  U_n=[U_n, I_n(entry)*rn];
endfor

times=[];
for entry = [1:1:steps],
  times=[times; entry*delta];
endfor

subplot (3, 1, 1);
plot(times, E_y, "-;Us;");
grid on;
subplot (3, 1, 2);
ax=plotyy(times, E_c, times, U_n);
grid on;
xlabel ("time, s");
ylabel (ax(1), "Uc");
ylabel (ax(2), "Un");
subplot (3, 1, 3);
plot(times, I_c, "-;Ic;");
grid on;
  • Volt1 - функция моделирующая нарастание напряжения от источника
  • R1_res - функция для моделирования электретного микрофона
  • dUc_dt - функция рассчета dU по dt для емкости.

Вот график моделирования:

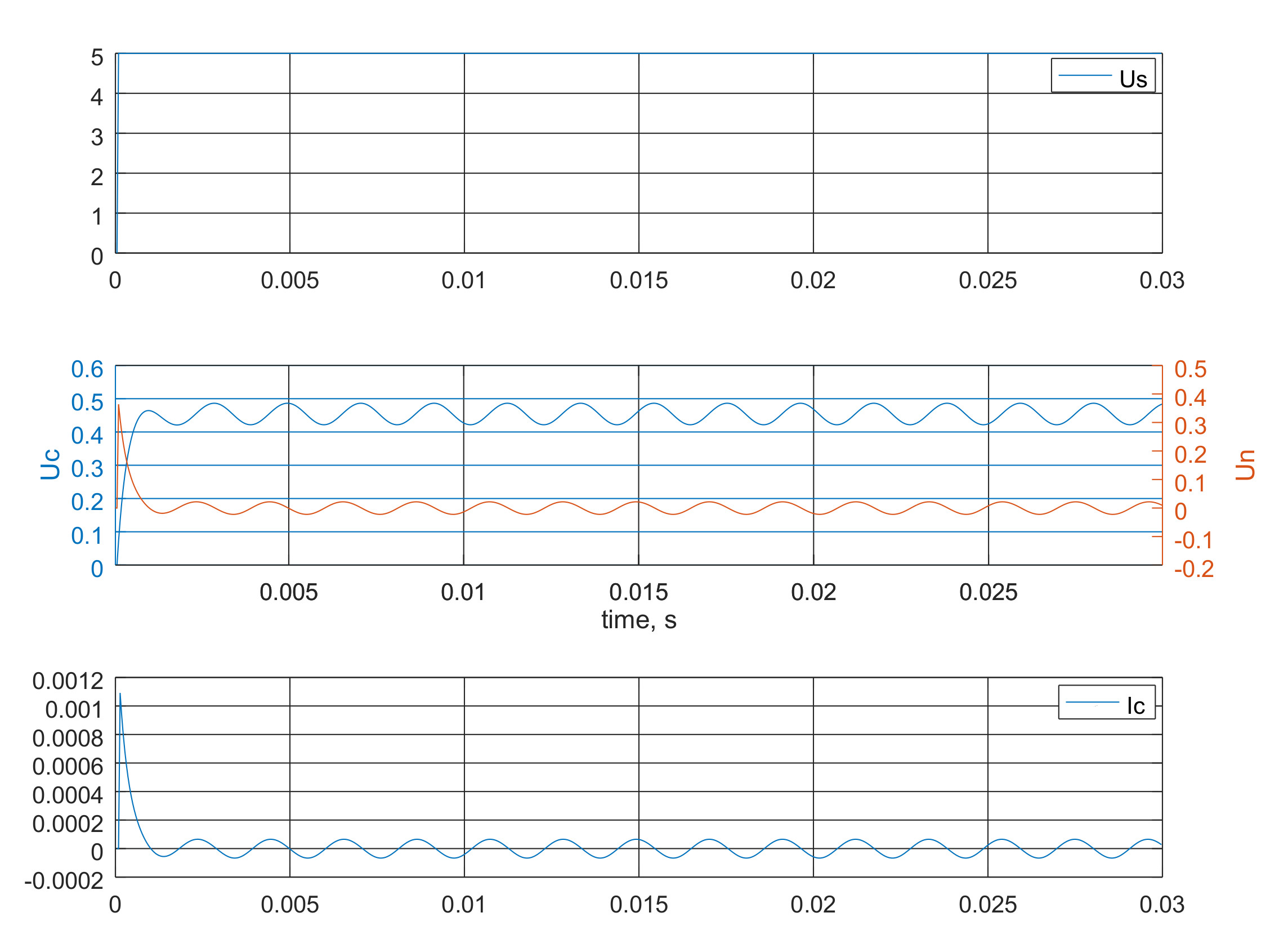
Octave

Вроде похоже на LTSpice.

А вот чуть модифицированное моделирование, когда резистор эмулятор выдает разную частоту изменения сопротивления, при понижении частоты уровень выходного сигнала уменьшается, при увеличении - увеличивается. Т.е моделирование показывает, что такая схема будет ослаблять низкие частоты, а вот с частотами выше 2000 Герц работает фактически без искажения.

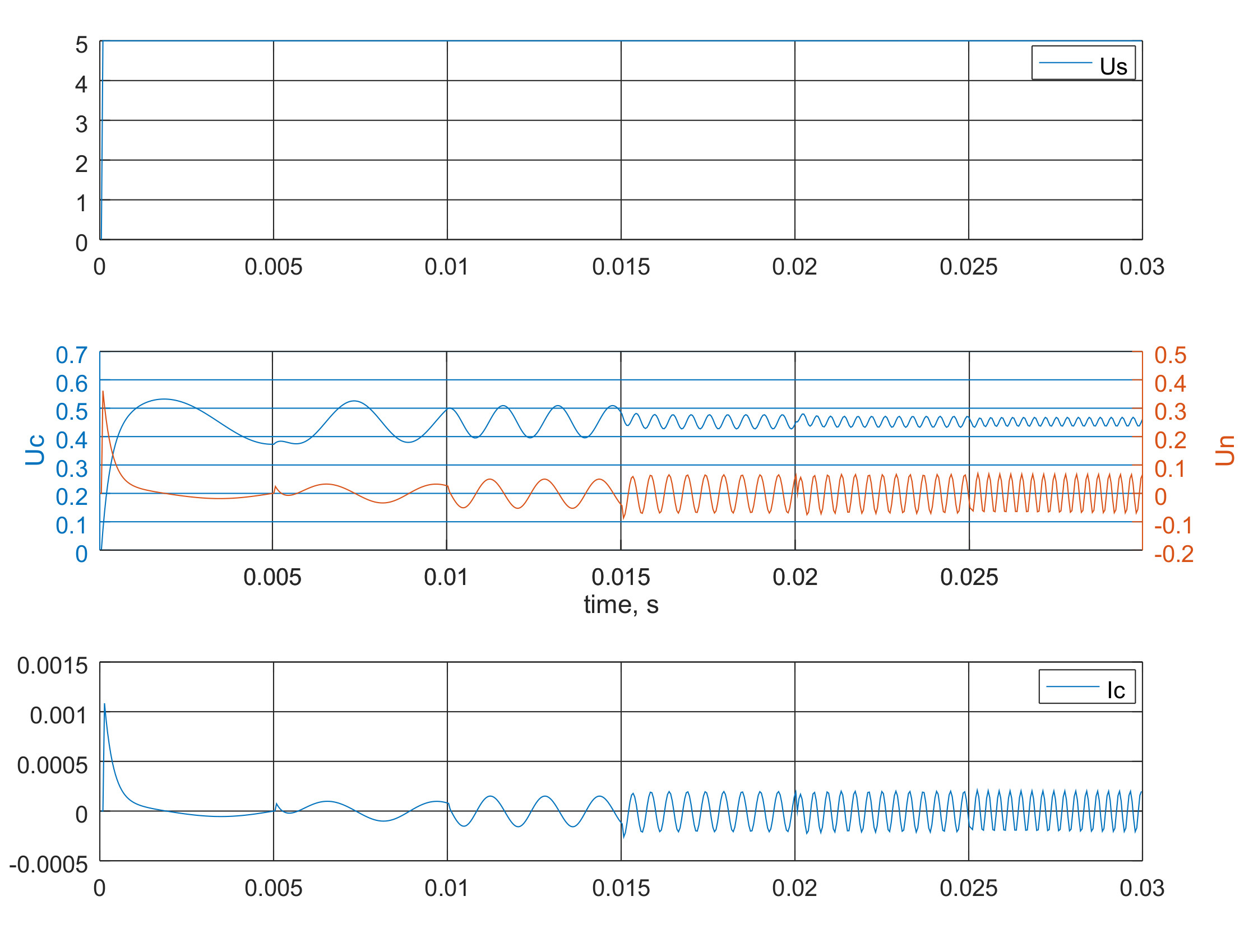
Octave 2

Вобщем, увеличении схемы до 3-х контуров привело к монструозным уравнениям. LTSpice все-таки солидно упрощает моделирование схем и судя по тому, что моделирование классическими формулами в математическом пакете совпали с LTSpice, его результатам можно доверять :).

Добавить комментарий

Следующая запись Предыдущая запись